FlappyMoonbird

FlappyMoonbird is a PvP Bird-themed Game World inspired by Moonbirds. The goal is to combine all kinds of excellent casual games with the Web3 ecosystem and build a metaverse of casual gamefi. The first Free to Earn casual chain game has been launched.
1. Racing Birds Brief:
Racing Birds is a game that rewards the brave. The global multi-bird match starts a group to see who is the last surviving bird. You may encounter various accidents here, but the final winner will get rich $FMB, Egg, Treasure boxes (BNB chain), Flappy birds NFT (BNB chain) airdrop, and other rewards.

Racing Birds will have three versions:
1.1 Entertainment version (SOLO):
Players can choose their favorite birds to compete with. During the competition, they can use props to hinder their opponents. The top three can get different rewards.

First place gets the golden egg; Second place gets a silver egg; Third place gets a rainbow egg;

1.2 On-chain version (ARENA):
In the pure chain version, the result of the game depends entirely on the hash value of blockchain data. Players who guess the result will get a lot of $FMB and airdrops. FMB racing bird random number calculation method:
1、Confirm the betting end time then click TS; 2、Take the last 10 digits of hash as H; 3、Convert H from hexadecimal to decimal and then take modulo 720 (720 is the total number of racing bird results), get result R; 4、R+1 is substituted into the backtracking algorithm of the two-dimensional array to get the race result.
Assuming we have a two-dimensional array $a$, where $a_{i,j}$ represents the element in row $i$ and column $j$. The backtracking algorithm usually uses a recursive function to traverse all possible solutions, with the following steps:
A. Define a recursive function with parameters including current row number $i$, current column number $j$, current state $s$. B. Check whether it meets the termination condition, if yes, return current state $s$.
C. Traverse all possible values of current column, assuming that current column value range is [1,n], there are n possible values. D. For each possible value, check whether it meets constraint conditions. If yes, add this value to current state $s$ and recursively call function to process next row. If not, skip this value directly. E. After recursive call is completed, backtrack to current state $s$ and try the next possible value.
In mathematical formula form, the recursive function can be expressed as $$ f(i,j,s) = \begin{cases} s & \text{if } \text{meets termination condition} \ \max_{k \in [1,n]} { f(i+1,j+1,s \cup {a_{i,k}}) } & \text{otherwise} \end{cases} $$
Where $s \cup {a_{i,k}}$ means adding element $a_{i,k}$ to current state $s$, $\max$ means taking maximum value for all possible states.

1.3 Strategy and Probabilistic Random Version (RACINGTRACK):
Based on the chain version added random events and attribute effects, random events include lightning strikes and gunshots. Attributes are Speed, Stability, and Luck. Players who guess the result will get a large amount of FMB and airdrop.
2. Gameplay
2.1 Entertainment version (SOLO):
Select the bird you want to participate in the game, you can choose corresponding props in the game to hinder opponents or make yourself speed up, use props at the right time, and let yourself win.

2.2 Fully on-chain Version (ARENA)
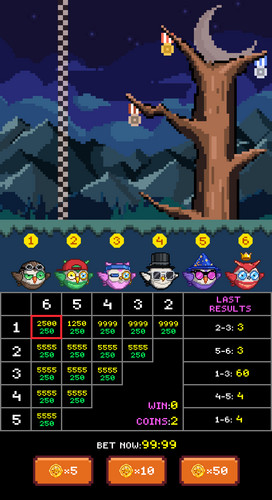
Choose one of the 6 randomly appearing birds or choose a ranking you agree with, for example, you can only choose the first place as bird 1, or you can choose first place is bird 1 + second place is bird 2 combination, you can choose up to guess 5 birds’ rankings. The more correct rankings you guess, the higher the odds, and the more generous the prizes.
2.3 Strategy and Probabilistic Random Version (RACINGTRACK):
Choose your favorite top two among birds 1 to 6, on the betting table value, yellow represents odds, pink represents global participation $FNB amount, and green represents player’s participation $FNB amount.
Clicking on each bird has a corresponding value reference, of course, a higher value means a higher winning rate but the corresponding return rate will be less.
3. Socials
Web: https://flappymoonbird.xyz/
Twitter: https://twitter.com/flappymoonbird
Discord: https://discord.gg/flappymoonbird
Linktree: https://linktr.ee/flappymoonbird